Computing a feedback system

Last week I was invited to Curiously Minded, where I prepared some code on how to compute a feedback system with webcam capture. As a result of the jam session, here is the codepen with source code

So, basically, this article intends to settle down some concepts and giving a further explanation of final code.

Introduction: feedback systems and analogic video-feedback

A feedback system, is one whose output is feed again into it creating a dependency between input-output signals.

If you have a camera connected to a monitor, when recording with the camera the screen the output signal being displayed is the recording of the screen itself, generating visual feedback loop. And slightly changes may create infinite corridors, and beautiful spirals. This process is known as video feedback.

This feeling of infinite nested screens, you might have experienced it in an elevator taking a selfie, and voilà! visual feedback there!

So we will be writing code to simulate something like that, but eventually trying to bring some glitter on the screen. If you are not so interested in Maths, you can jump implementation!

Extra mathemagical motivation

The beauty emerging from nature's complex patterns are usually described with partial differential equations. Their solutions are visualized as points in a multidimensional space, and it's called phase space or state space.

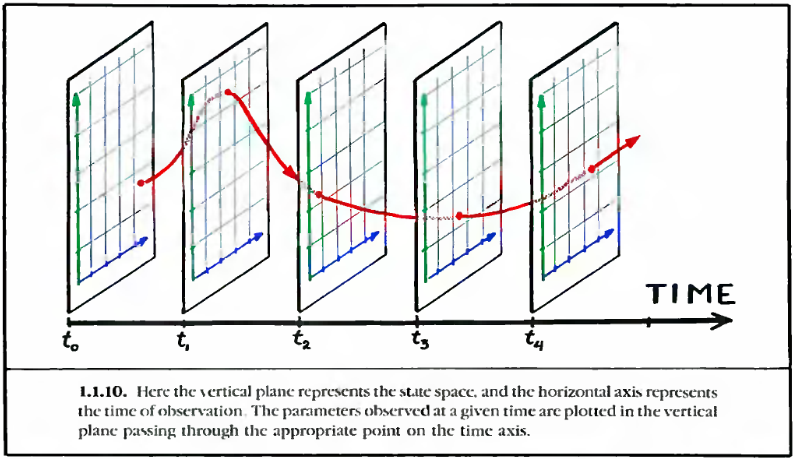
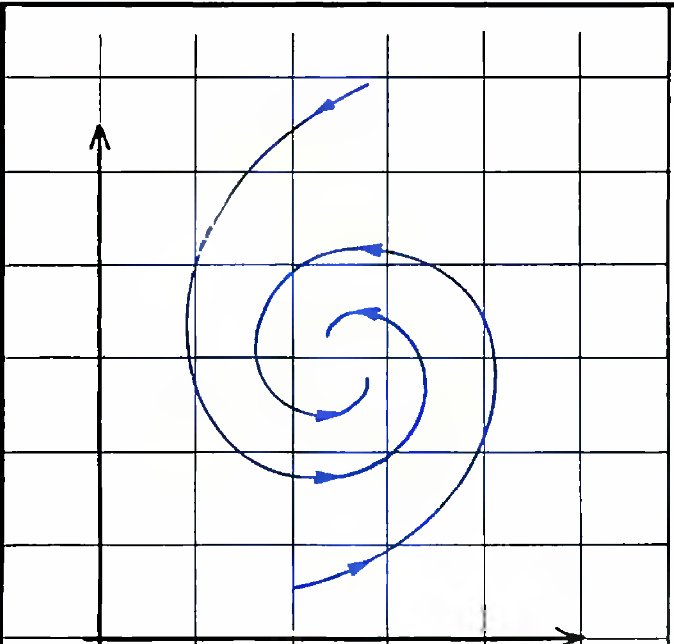"The space of states may be imagined to flow, as a fluid, around in itself, with each point following one of these curves. This motion of the space within itself is called the flow of the dynamical system."[1]

We should think of dynamical systems as the set of rules that determine behavior.

So feedback systems, as well as cellular automatons, are used for describing behavior.

Video feedback eventually is a good model for studying dynamical systems ( non-linear dynamics ). I was first introduced to it while reading CHAPTER 5 - I am a Strange Loop.

But did not dive into deep study, until I saw Olivia's video introducing hydra and referenced this paper: Space-time dynamics in Video Feedback. And while I was in NYC, I had the privilege to learn with maths' wizard Andrei Jay who wrote this article, for having a deeper understanding of videofeedback concepts. And also Softology has lots of useful references.

Eventually computing feedback systems enables us to explore and study non-linear dynamics.

Extra links and references

• [1] The Geometry of behavior - Ralph H Abraham
• YouTube - Space-Time Dynamics in Video Feedback
• Cellular Automata, PDEs and pattern formation
• Non Linear dynamics of video feedback
• Pattern formation in non equilibrium physics

Computing a "video-feedback" system

“As might be expected, all the unexpected phenomena that I observed depended on the nesting of screens being (theoretically) infinite — that is, on the apparent corridor being endless, not truncated..."
by Douglas Hofstadter, "I am a Strange Loop"

How do we compute infinite nested screens? Our digital world, implies considering time discrete, as steps. So that is how I think when designing a visual feedback system. Like a sequece of frames, affected by an algorithm at each frame-step.

Frame by frame

For that we set up camera, renderer and main scene in Three.js.
And create a plane object with shader material, who is the container of frames. The shader material will compute an action, that will generate changes on the pixels at each frame.

ACTION: Fragment shader

So, the objective is to implement an algorithm that updates pixel color based on information of previous frame {pixel itself and the neighborhood }.

This is a visual explanation:

Assuming we can access to previous frame (we can call it previous state), in our codepen example, we are making a weighted average of:

• pixel: multiply by scalar
• north, south, east and west diections: multiply by a vector (each RGB channel has a special weight, so you can eventually experiment different diffusion rates on each color)
• northeast, northwest, southeast and southwest directions: multiply by other scalar

Scalars will define how much does the pixel is influenced by it neighbors ( This approximates the Laplace operator, which measure divergence of color)

Then explore different ways of altering pixel color: using the calculated Laplacian, and webcam capture. These eventually "encode" the rules of the system.

Also, as when we think in fragment shaders, we essentially have this idea of: receiving position of pixel and returning color; and paralelizing this procedure for all pixels at the same time. But pixels are memoryless, so we need to preserve the previous frame as a uniform variable.

At this point, we see how we need shared information between frames.

For that we will be using a technique call Ping Pong Buffers.I was first introduced to this technique with this article on how to compute a smoke shader.

Implementing it on Three.js:

NOTE 1: the action/algorithm I will be using in the gifs/examples below will be a simple color swap.

NOTE 2: In the codepen, the animation function has 3 options for rendering, which are explained below. Make sure to uncomment one at a time.

Idea 1: Use buffer to precompute next frame

How it works would be: we will be having two sequences of frames: the main one, which will be displayed in the canvas, and the buffer one.

At each, frame-step, buffer scene applies color swap to frame from main scene.

What is a frame-step?

Observe that the requestAnimationFrame is calling the animate function, which it's calling the renders functions. So, at each frame-step we are executing a render function.

This first idea maps to render_1.

The big picture of what is doing is:

• rendering the buffer scene (applying action)
• using previous frame to map it to main scene

The buffer scene is precomputing next frames.

See the following gif to understand how eventually the Ping Pong technique works:

What we should we aware is that the action (which in this example is swapping colors) is ocurring in the main scene, this means, the system is working as expected.

And at each frame-step the last frame of buffer scene, is eventually what would be read on the main scene in the next call.

As I generally like exploring different paths through the same target. I came up with this second idea:

Idea 2: Use buffer to preserve last frame

So here is visual representation of it:

It is very similar to the other one, but instead of main scene reading from buffer scene, the buffer scene is writing from previous main scene's frame. And main action(swapping color) is being executed on the main scene.

WHY WOULD YOU DO SOMETHING LIKE THAT?

Well, I wanted both scenes to be mapped to an action, so eventually there are more shaders to code.

Or having each sequence of frames associated to an action can make the system more interesting :)

So, let's rename our sequence of frames:

• Main Scene -> Copy Action Scene
• Buffer Scene -> Swap Action Scene

And would eventually behave the same (which in this example is swapping colors).

The first implementation of this idea maps to render_3:

And also had a bug

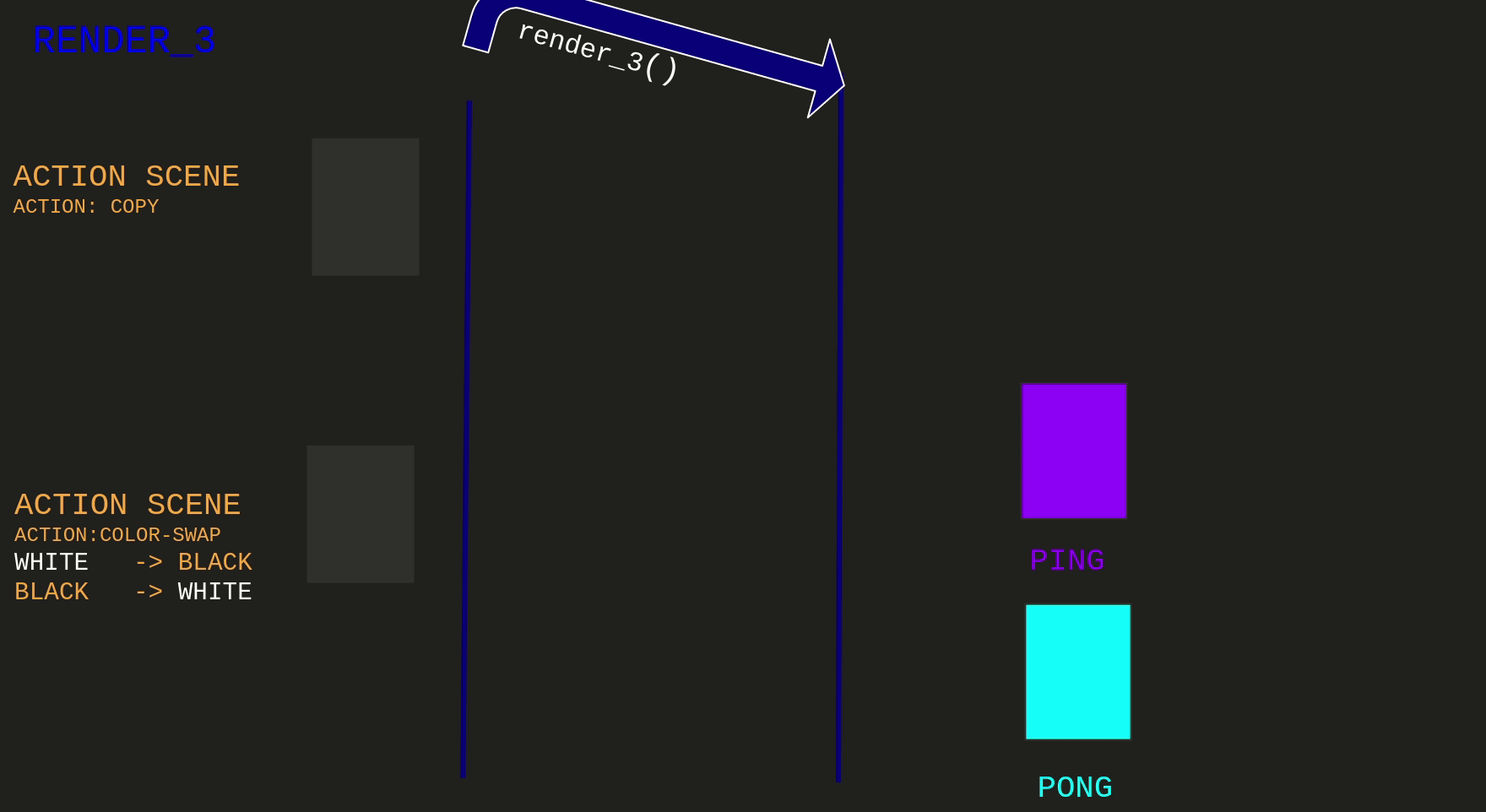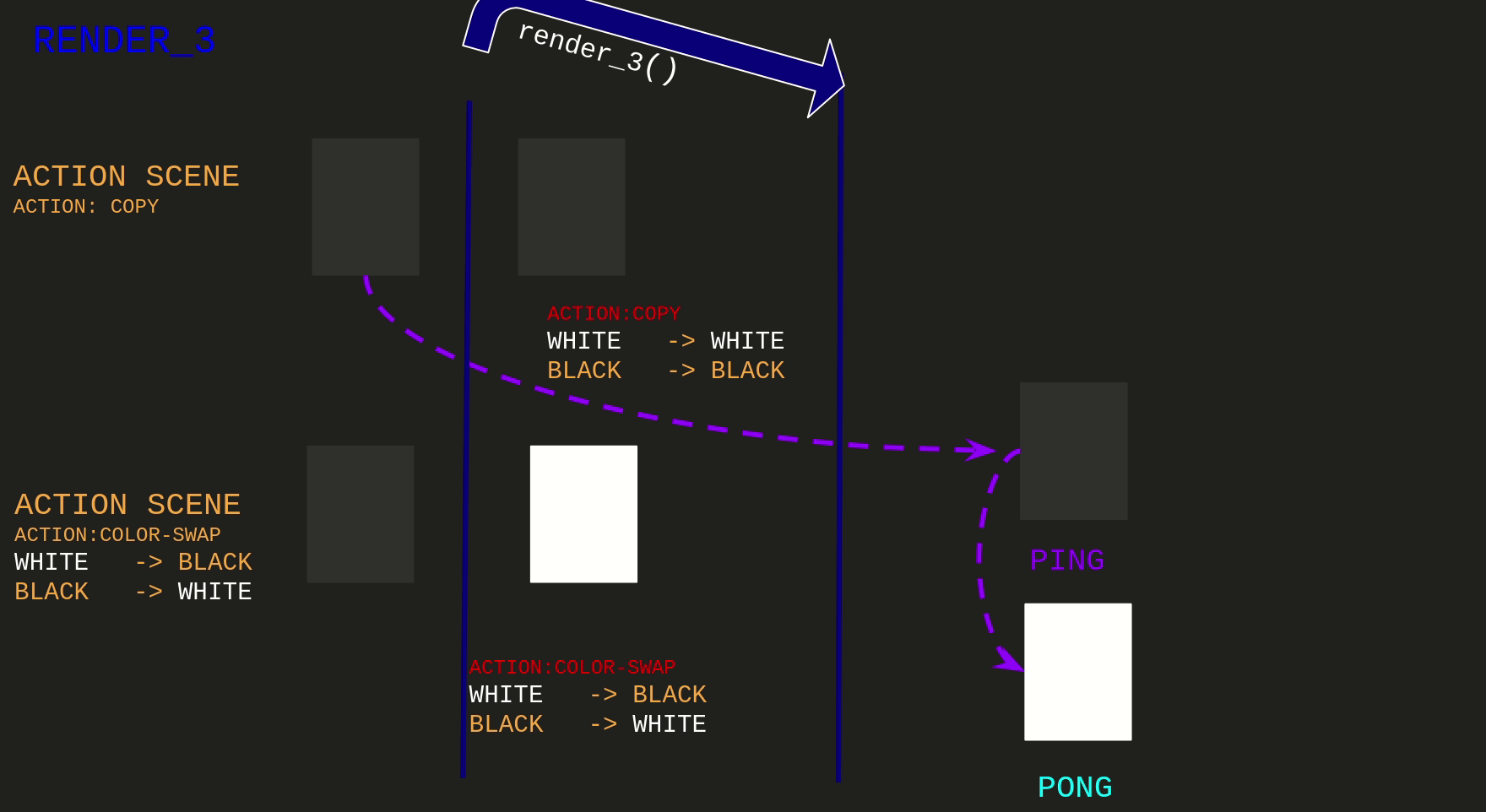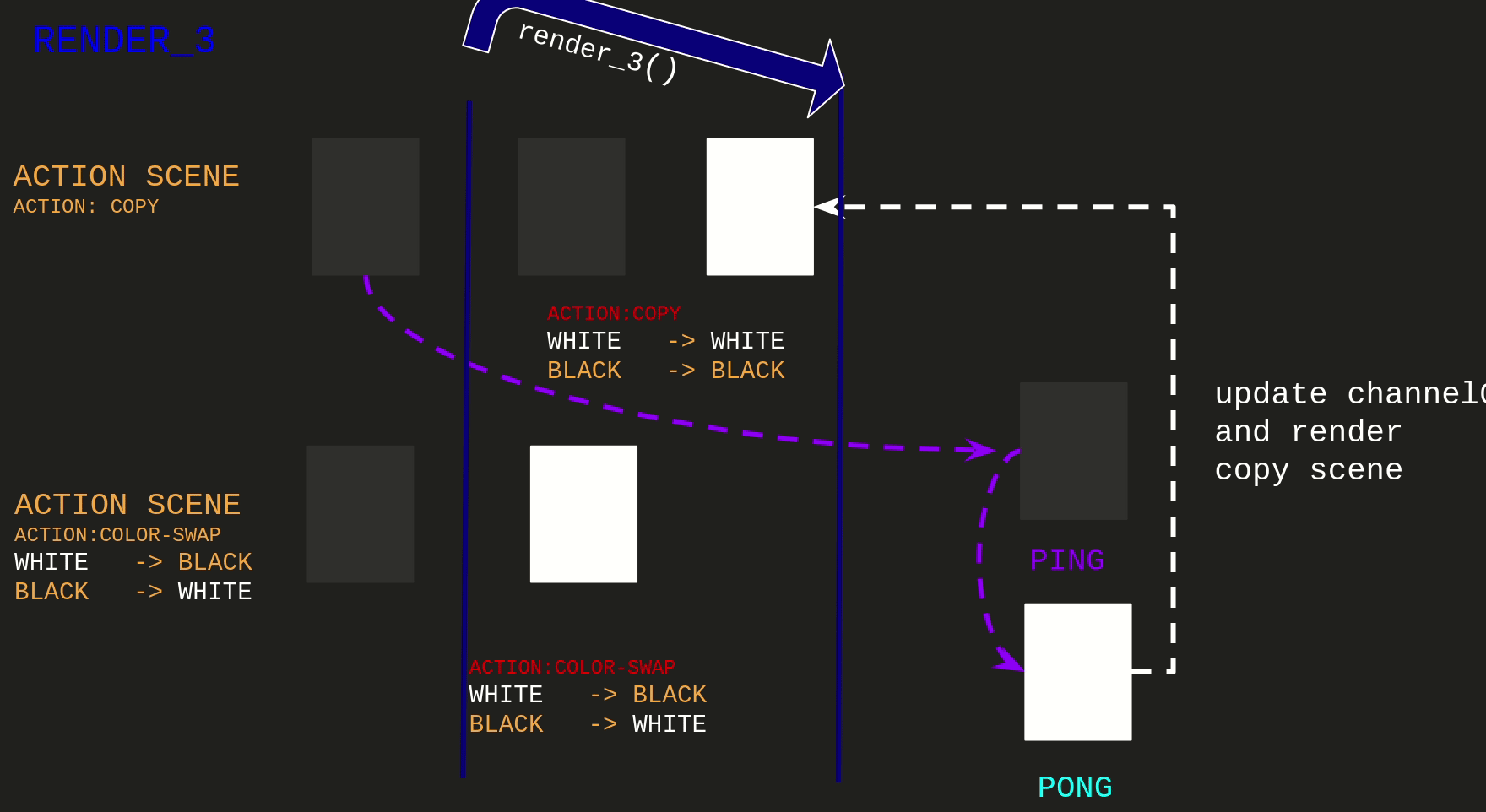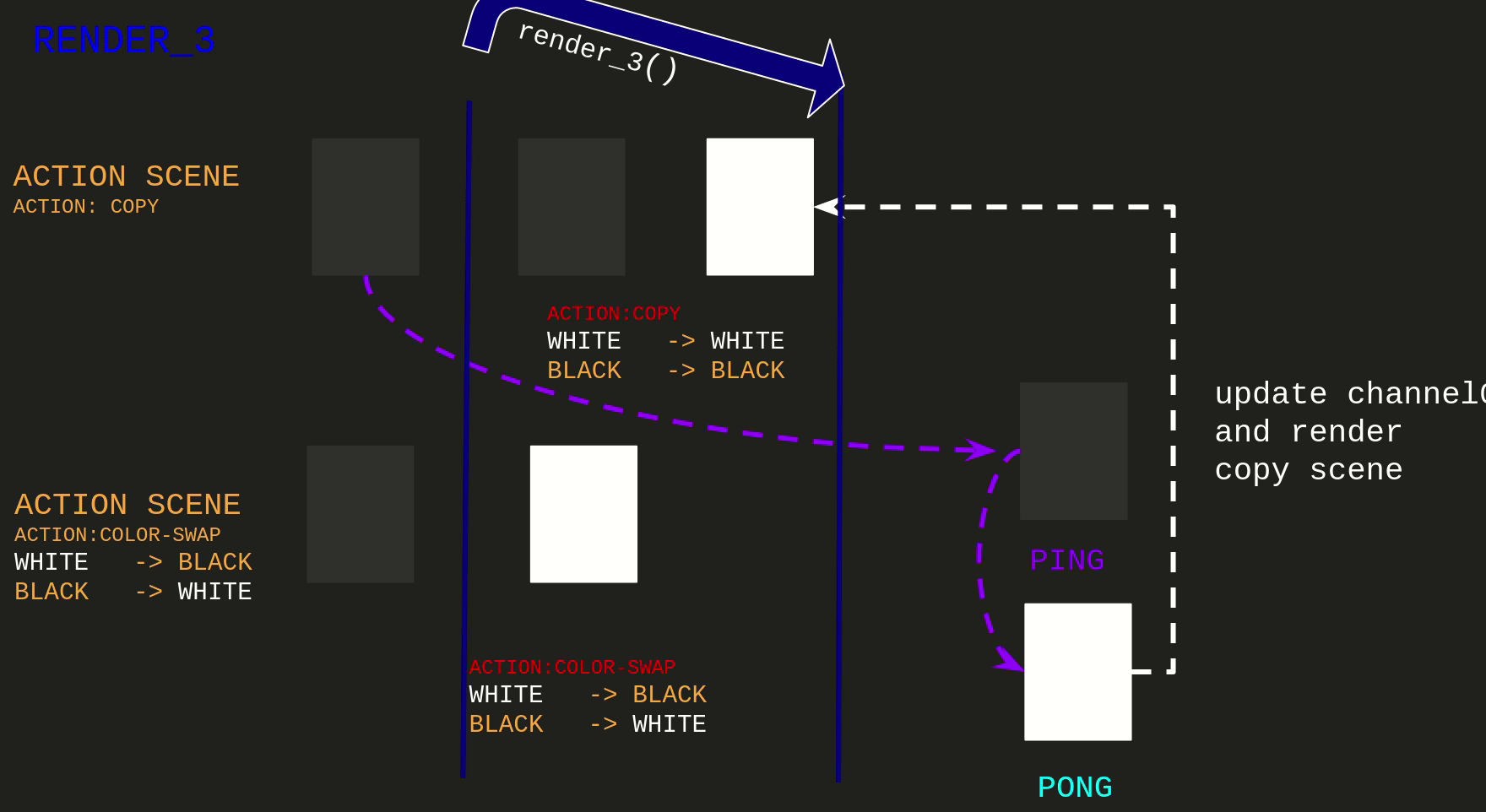
For being able to write I was rendering another frame of the Copy Action Scene, saving it to ping texture. And the Swap Action Scene is using the ping as the back buffer for computing next state.

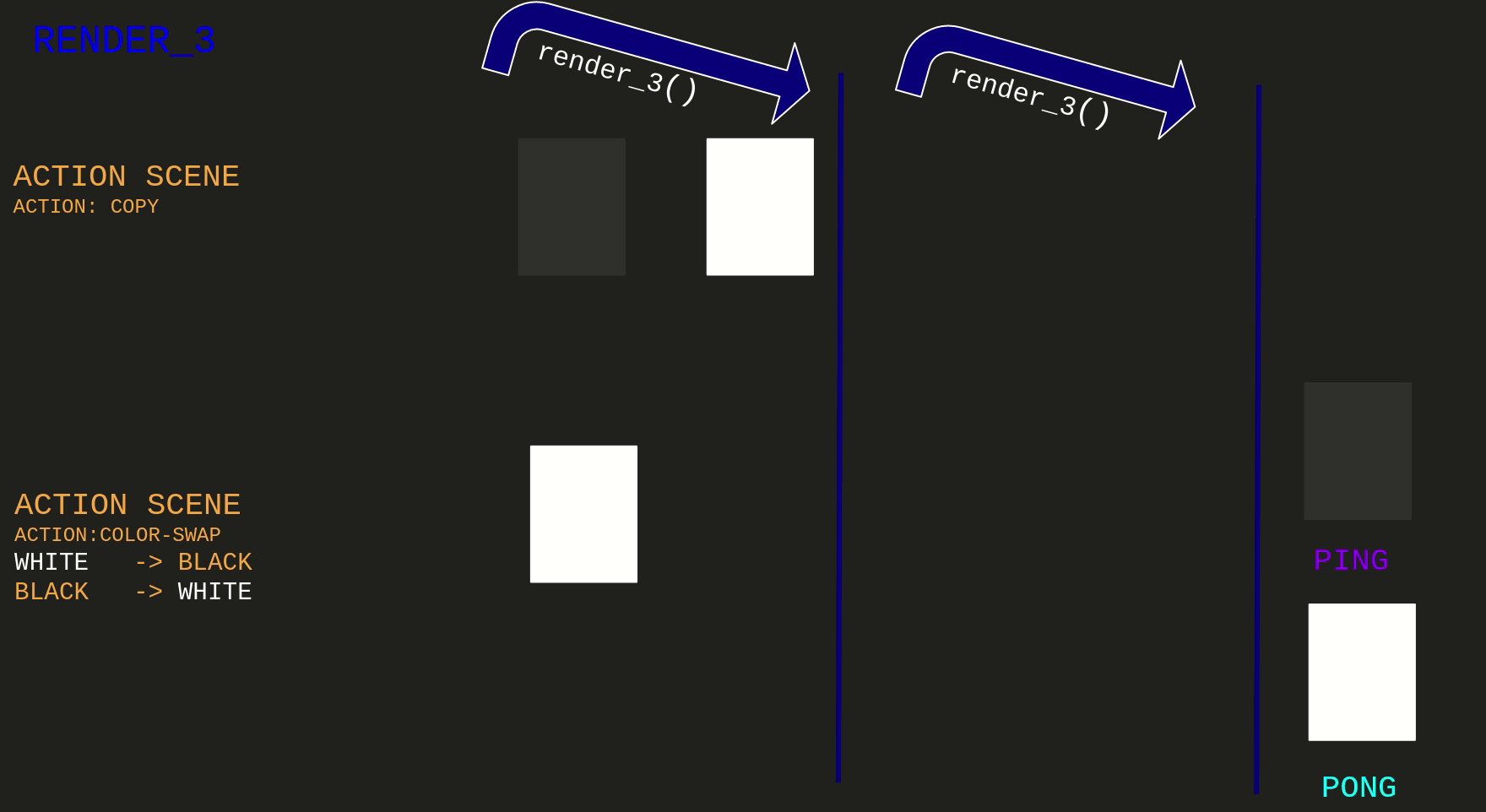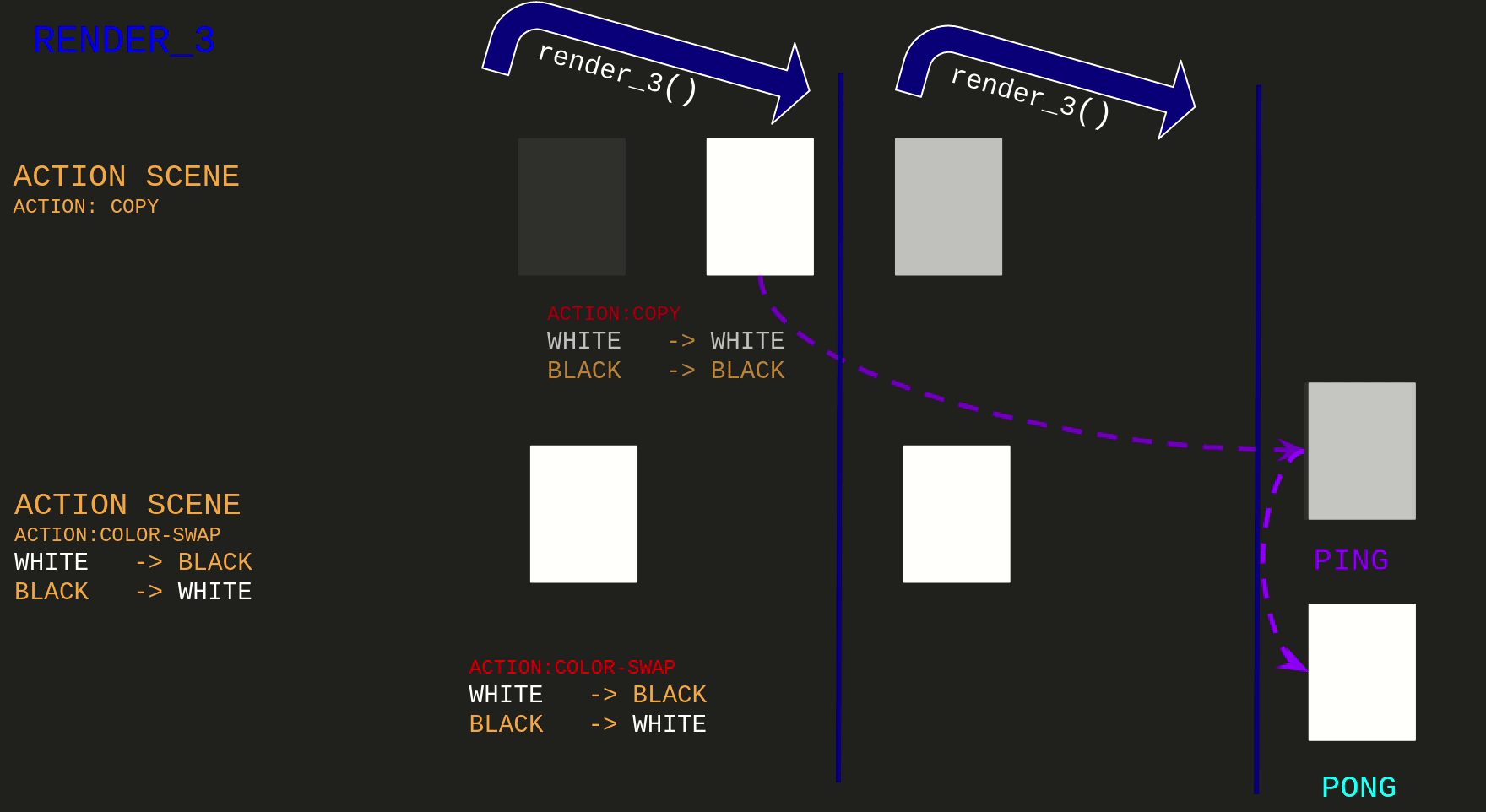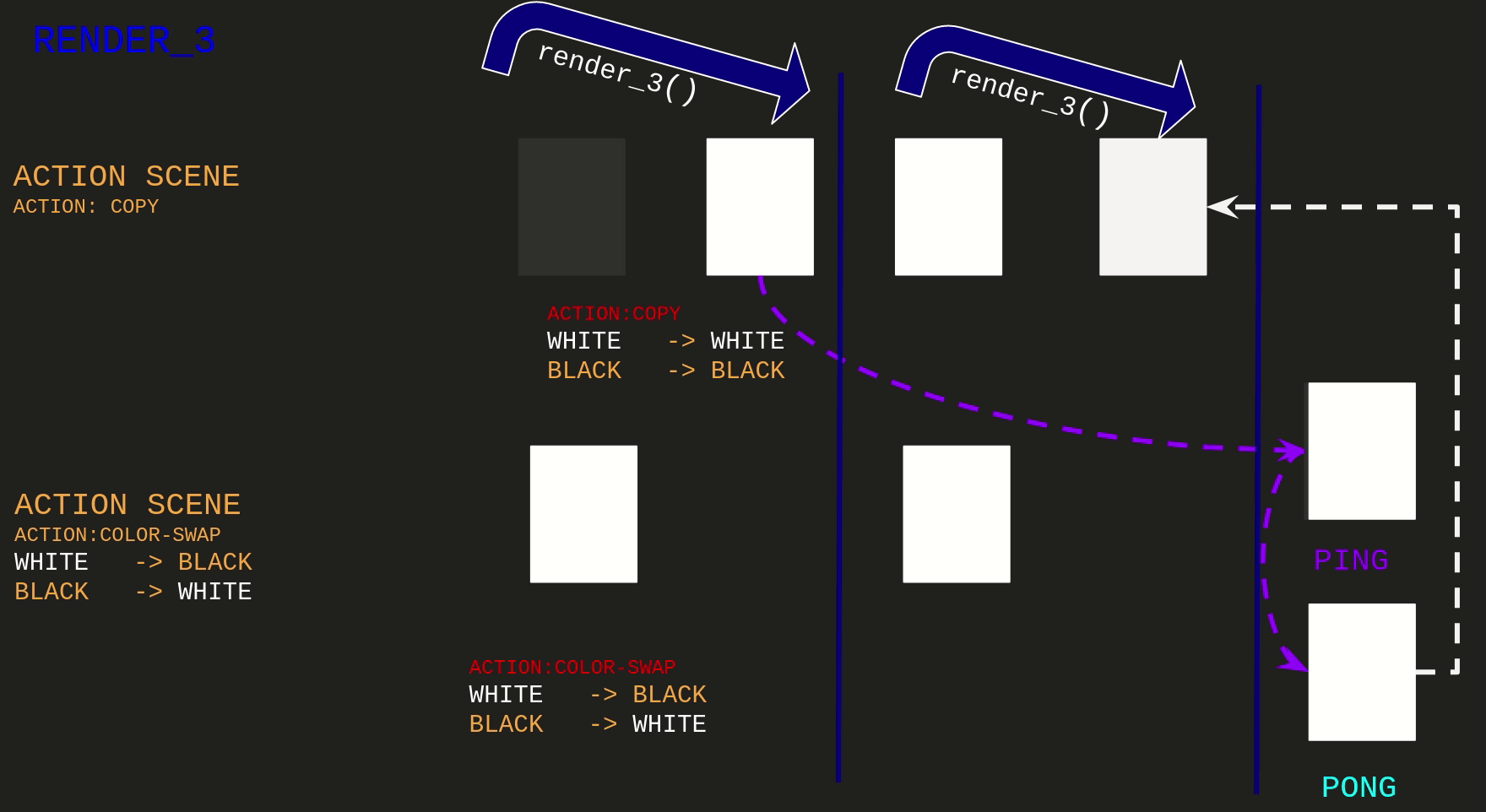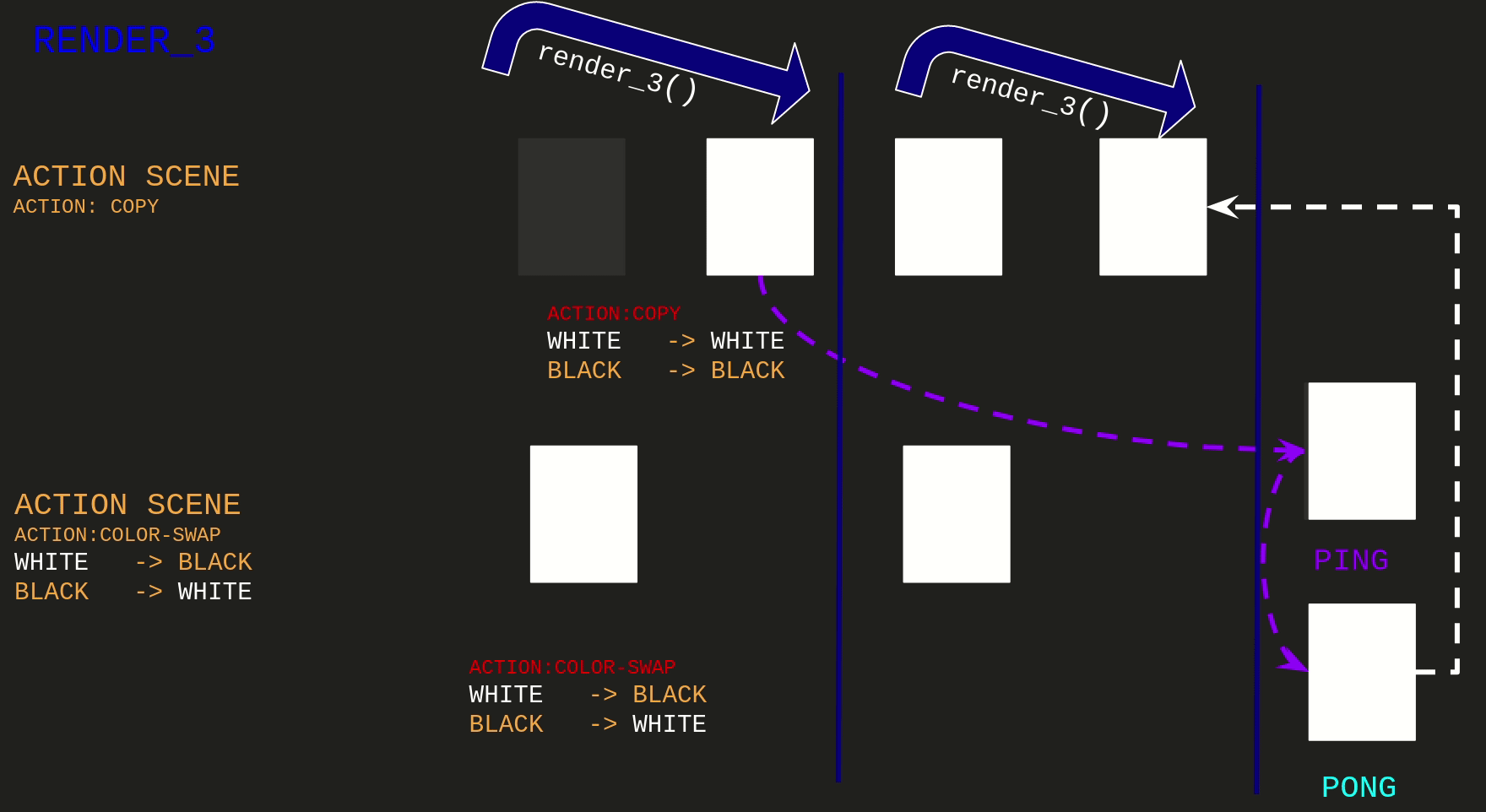
Observe that the Copy Action Scene is not having the overall behavior we would expect that is: swapping colors on the frames at the end of the render_3 call.

Alternative to how can be approach it

After realizing that is was not eventually working as expected.

I came up with the idea of:

• Main scene would always read from buffer.
• Buffer scenes will be asociated to an action, in this case, copy and swapping. But eventually they both have fragment shaders (and potentially could be any shader you want).

And introducing an alt texture will allow us to:

• apply the copy action from last swap's frame and story in alt
• apply the swap action from last copy's frame and store it in ping
• swap textures
• main scene reads from ping

This idea maps to render_2:

Conclusion

For designing feedback systems you have 2 worlds to explore:

• Shader side of the code: fragment shaders algorithms. See more examples you can eventually implement with a feedback system

• Javascript side of code: deciding how many buffer scenes you want to have and how frames interact, at each render-step of your discrete system. This is a new superpower for me 💕

And also, when computing, remember that understanding bugs might always lead to new portals.

I took this quote from Chapter 2: On Creativity of Pygmalion - Creative Programming Environment by David Canfield Smith

Of course errors might depend a lot in context, there are scenarios that we don't really want bugs. But in this case, I think it is a good one.

When learning, having curiosity for alternative paths that may be more intuitive for you, encourages you to explore unknown scenarios, and looking for answers of what if...??s would eventually make you have a wider knowledge of what you are trying to learn.

Further directions

Writing this article I discovered that Three.js has GPU Computation Renderer that might be another solution for bug fixing :)